この記事では数値計算によく使われるPythonのライブラリであるnumpyで行われている数値計算をよりよく理解するために,ブロードキャストを学習します.これを知ってるか知らないかでnumpyを使っているコードの理解度が全く変わってくるので,しっかりと理解しましょう.
numpyの基本と行列・ベクトルの計算はこちら
numpyでよく使う機能まとめはこちら
ブロードキャスト
ブロードキャストとは配列同士のshapeが一致していなくても,うまくshapeを計算できる形に合わせて計算できるようにする機能です.
numpyを使って高次元のndarrayの数値計算を行うとき,データの形がぴったり同じでなくても,うまく整合性を保って計算をしてくれたら便利なときはたくさんあります.numpyではブロードキャストという機能を使ってそれが可能になるのです.
こちらの公式サイトにはブロードキャストをする際のルールは4つあると書かれています.
この記事ではその4つのブロードキャストのルールについて,例を交えながらわかりやすく紹介していきたいと思います.
ルールだけ見ると少しわかりづらいと思うので,よくわからなかったらすぐ下の例を読んでください.自分でコードを書くとさらに理解が深まると思います.最後に確認クイズもあるので,理解を深めるためにトライしてみて下さい.
ルール1:対象の配列の中で次元数が一番大きな配列より次元数の小さな配列は全てshapeの先頭に1を入れる
例を見ていきましょう.
# rule 1
a = np.ones((1, 3, 2))# shapeが(1, 3, 2)の要素がすべて1のndarray
b = np.ones((3, 2))# shapeが(3, 2)の要素がすべて1のndarray
c = a + b
print('aの次元', a.ndim)
print('bの次元', b.ndim)
print('cの次元', c.ndim)
print('cのshape', c.shape)
print('cの中身\n', c)
'''
出力結果:
aの次元 3
bの次元 2
cの次元 3
cのshape (1, 3, 2)
cの中身
[[[2. 2.]
[2. 2.]
[2. 2.]]]
'''
上の例では「a」の次元は3,「b」の次元が2となっており,次元が違うデータ同士のため,本来であれば計算ができなそうです.
ここでブロードキャストが働きます.今,一番大きな次元数が3で「b」の次元数が2なので「c = a + b」の部分ではbのshapeの先頭に1が追加されshapeが(1, 3, 2)の配列として扱われるのです.
「c」のshapeを見てもらえばわかる通り計算結果はやはり(1, 3, 2)というshapeになっており,中身を確認するとしっかりと和が計算されているのがわかります.
ルール2:出力される配列の各次元の要素数(shape)は対象となる配列の各次元の要素数のなかで最大のものになる
# rule 2
a = np.ones((1, 2, 3))# shapeが(1, 2, 3)の要素がすべて1のndarray
b = np.ones((3, 2, 1))# shapeが(3, 2, 1)の要素がすべて1のndarray
c = a + b
print('cの次元', c.ndim)
print('cのshape', c.shape)
print('cの中身\n', c)
'''
出力結果:
cの次元 3
cのshape (3, 2, 3)
cの中身
[[[2. 2. 2.]
[2. 2. 2.]]
[[2. 2. 2.]
[2. 2. 2.]]
[[2. 2. 2.]
[2. 2. 2.]]]
'''
上では「a」と「b」の次元は両方3,shapeはそれぞれ(1, 2, 3) と(3, 2, 1)となっています.
今,出力である「c」のshapeを考えるときは「a」と「b」のshapeを比べて各次元の要素数のうち大きい方が出力のshapeに反映されます. (1, 2, 3) と(3, 2, 1) の比較は図にすると下のような感じです.
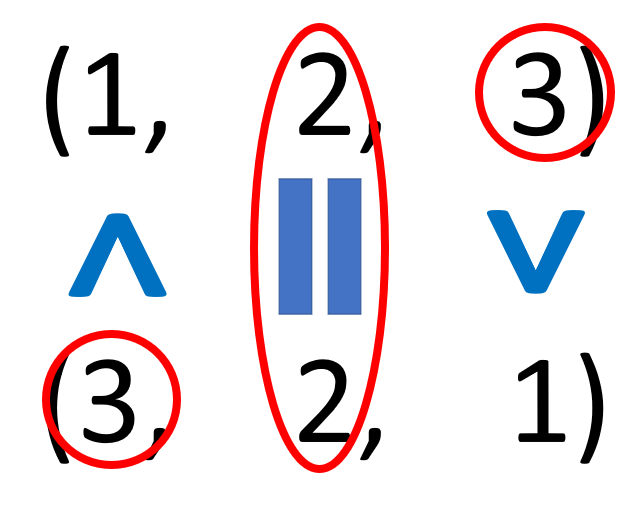
print関数で出力した結果から,「c」のshapeが(3, 2, 3)になっているのがわかります.
ルール3:配列の各次元の要素数が一致しているか,1のとき,それらの配列は計算することができる
# rule 3: 計算できる例
a = np.ones((1, 3, 4, 1))# shapeが(1, 3, 4, 1)の要素がすべて1のndarray
b = np.ones((3, 1, 4, 5))# shapeが(3, 1, 4, 5)の要素がすべて1のndarray
c = a + b
print('cのshape', c.shape)
'''
出力結果:
cのshape (3, 3, 4, 5)
'''
以上の例では各次元の要素数を見てみると0, 1, 3次元はどちらかの要素数が1となっており,2次元目は要素数が4で一致しているのがわかります.出力のshapeはルール2と組み合わせた結果(3, 3, 4, 5)となります.図は以下.要素数の内大きい方を赤丸で囲み1に青い下線を引きました.
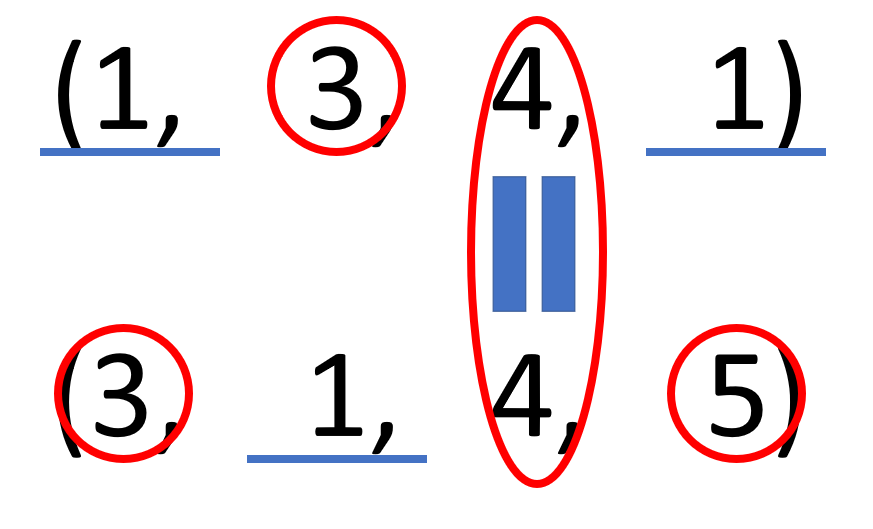
計算できない例も見ておきましょう.
# rule 3: 計算できない例 a = np.ones((2, 3, 2)) b = np.ones((3, 3, 2)) c = a + b ''' エラー: ValueError: operands could not be broadcast together with shapes (2,3,2) (3,3,2) '''
以上では最初の次元の要素数が「a」は2,「b」は3となって異なっていてどちらも1でないことから計算ができません.エラーをみてもshapeが(2,3,2)と (3,3,2) の足し算はブロードキャストできませ~んと言っています.
ルール4:次元の要素数が1でブロードキャストがなされる場合,同じ値を繰り返す
ルール3では各次元の要素数が1のときはブロードキャストされ計算できることを説明しましたが,計算される際は同じ値を繰り返し用います.
# rule 4
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])
c = a + b
print('aのshape', a.shape)
print('bのshape', b.shape)
print('cの中身\n', c)
'''
出力結果:
aのshape (2, 2)
bのshape (1, 2)
cの中身
[[ 6 8]
[ 8 10]]
'''
以上では「a」のshapeが(2, 2)で「b」のshapeが(1, 2)なので「b」の最初の次元は同じ値を繰り返ししようすることになります.上で行われている計算のイメージは以下のような感じです.
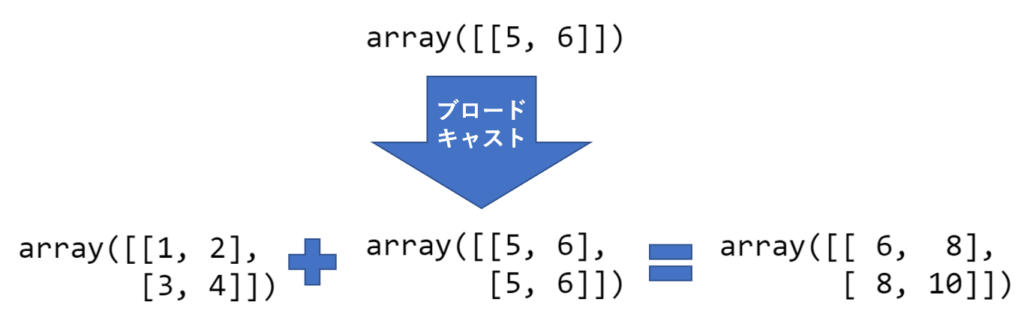
確認クイズ
以下のコードを実行した結果,何が出力されるか考えてみてください.ヒントもあります.
考えたら実行して答えを確認しましょう.
# ヒント:ルール1とルール2 a = np.ones((2, 2, 3)) b = np.ones((2, 3)) c = a + b print(c.shape)
# ヒント:ルール1とルール2 a = np.ones((2, 2, 3)) b = np.ones((3)) c = a + b print(c.shape)
# ヒント:ルール1とルール3 a = np.ones((2, 2, 3)) b = np.ones((3, 3)) c = a + b print(c.shape)
# ヒント:ルール4 a = np.array([[1, 2], [3, 4]]) b = np.array([[5], [6]]) c = a + b print(c)
次回
次回は「matplotlib:プロット,散布図,ヒストグラムなど」について学習します.
次の記事はこちら.
機械学習のためにしっかりとPythonを勉強したいなら,ある程度の基礎を身に着けた後に下の本を読むのがお勧めです.この本をこなせば,より高いレベルへ到達できるでしょう.
